Quando si progettano macchine automatiche lo studio dei cinematismi, o comunque delle movimentazioni in genere, può assumere aspetti critici se le masse in gioco sono considerevoli e/o la ciclica del sistema è piuttosto rapida. Un approccio comune è quello di calcolare le rampe di velocità come ad accelerazione costante, ossia dividendo il Delta-V per il tempo in cui questo avviene.
In genere questo approccio, seppure scorretto formalmente, permette tuttavia di portare a casa il risultato senza grossa fatica o spremimento di meningi. Andiamo però a capire un po’ più in profondità cosa succede:
le forze d’inerzia a cui e’ sottoposto un meccanismo sono, nel caso più semplice, del tipo F=m*a. Ora, consideriamo che nel caso di rampa ad accelerazione costante abbiamo un momento in cui passiamo da un accelerazione nulla ad un momento successivo in cui questa diventa improvvisamente diversa da zero, e magari molto diversa da zero! Lo stesso farà quindi la forza d’inerzia che si oppone al moto. L’effetto finale sarà quindi una discontinuità nell’applicazione delle forze, e quindi nella migliore delle ipotesi avremo una vibrazione, ma in casi gravi potremo andare a sollecitare in maniera impropria i membri del cinematismo e portarli verso una fine prematura della loro vita utile.
Sopra scrivevo che in genere va tutto bene, e non si vedono quasi mai sorgere grossi problemi: questo dipende dal fatto che queste discontinuità e vibrazioni insorgenti vengono di solito assorbite da membri flessibili della catena cinematica: una trasmissione a cinghia, un giunto a stella, un motore azionato da inverter, etc. In altri casi non siamo così fortunati e dobbiamo studiare delle rampe di accelerazione e rallentamento più accurate.
 |
 |
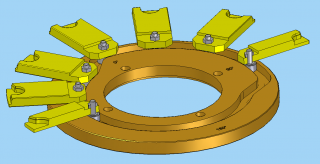
In passato sono stato incaricato di studiare delle camme per macchine ad alta velocità (circa 75 cicli/minuto), per dei cinematismi che dovevano partire da un punto e giungere ad un altro punto, e lì arrestarsi per un certo tempo. La prima cosa da fare è stata documentarsi in letteratura, dalla quale si ricavano vari insegnamenti, dei quali il più comune e condiviso è quello di realizzare delle camme con legge di moto polinomiale del 5° ordine, ossia del tipo:
y = a*x5 + b*x4 + c*x3 +d*x2 +e*x + f
dove y e x sono spostamenti sul piano.
La formula si può semplificare presto, considerando che imponendo spostamento, velocità e accelerazione nulle per x=0, si ottiene che i coefficenti f, e, d sono nulli.
Resta quindi la formula semplificata:
y = a*x5 + b*x4 + c*x3
che derivando una volta per ottenere la velocità diventa:
y’ = (1/5)a*x4 + (1/4)b*x3 + (1/3)c*x2
E derivando ancora una volta per ottenere l’accelerazione diventa:
y” = (1/20)a*x3 + (1/12)b*x2 + (1/6)c*x
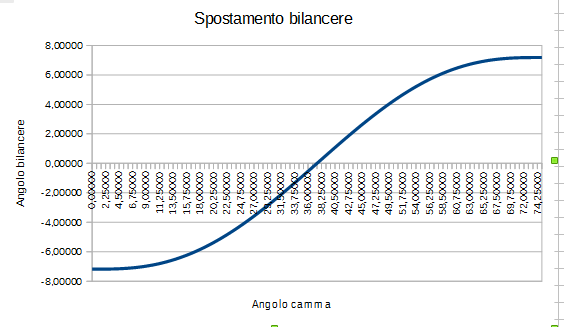
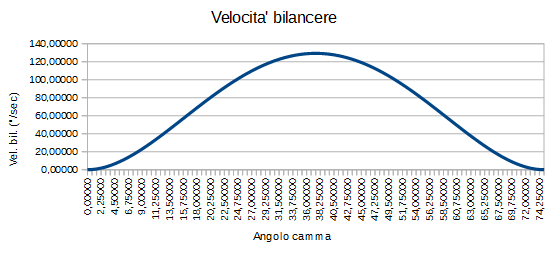
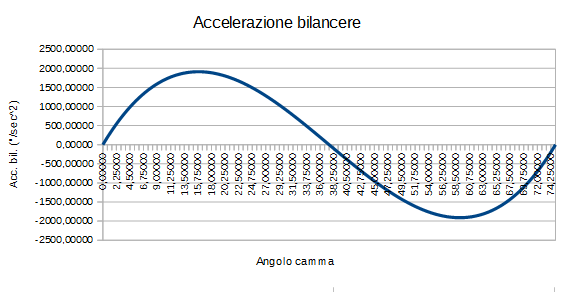
Ora vediamo che l’accelerazione è effettivamente nulla al punto iniziale, e si ricava, con le opportune equazioni messe a sistema, che è nulla anche al valore finale della nostra corsa, ossia quando y’ sara’ diventata nulla perchè arrivati a fine spostamento. Mettendo in grafico queste informazioni, abbiamo andamenti simili a quelli riportati nelle immagini:
|
|
|
|
|
|
E’ interessante notare l’andamento dell’accelerazione del cedente che si annulla a meta’ corsa, ossia quando il sistema comincia a rallentare per approssimarsi al termine del movimento. Come era stato previsto comunque, l’accelerazione varia con continuità nelle fasi di partenza e arresto, e quindi così faranno anche le forze d’inerzia che andranno ad incidere sui diversi membri della catena cinematica. Grazie a queste variazioni dolci delle forze di inerzia, altrettanto dolce e lineare sarà il funzionamento della macchina, senza antipatici urti, rumorosita’, ticchetti o vibrazioni, a tutto vantaggio della durata del sistema nel tempo.